Have you ever found yourself staring at a circle diagram, wondering how those lines and angles are related? That’s where the exciting world of secants, tangents, and angle measures comes in. These concepts are crucial for understanding the geometry of circles and unlocking a deeper understanding of how shapes work within our physical world.
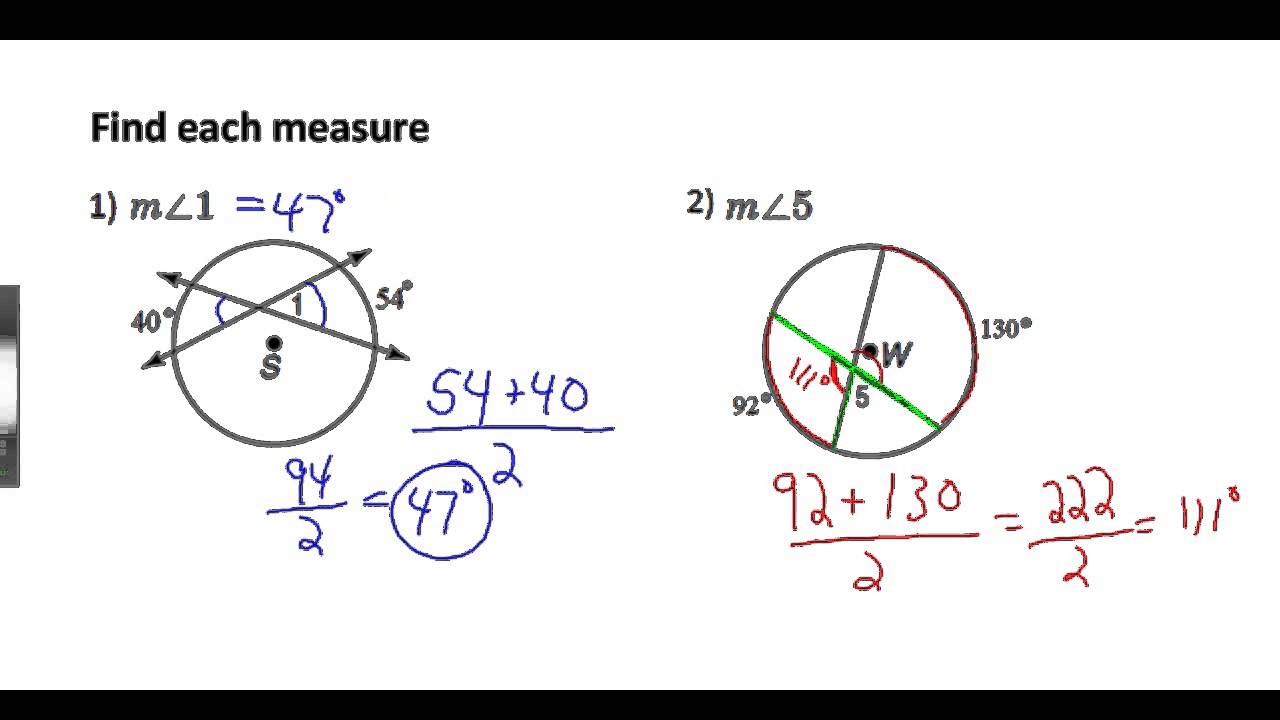
Image: www.youtube.com
Learning about secants, tangents, and angle measures isn’t just about memorizing formulas; it’s about developing a visual intuition for how these relationships play out in real-world situations. From designing circular structures to understanding the paths of satellites, these concepts prove their worth in various applications.
Delving into the Fundamentals: Secants, Tangents, and Angles
Secants: Cutting Through the Circle
Let’s begin with secants. Imagine a line that intersects a circle at two distinct points. That line is called a secant. Think of it as a straight road cutting through a circular park, touching the park at two points. A secant also forms two arcs within the circle, each having a unique angle measure.
Tangents: A Single Touch
Now, envision a special type of line called a tangent. A tangent touches the circle at exactly one point, grazing its surface. Picture a train track running alongside a circular lake, just touching the water at one point – that’s a tangent. The point where the tangent touches the circle is known as the point of tangency.
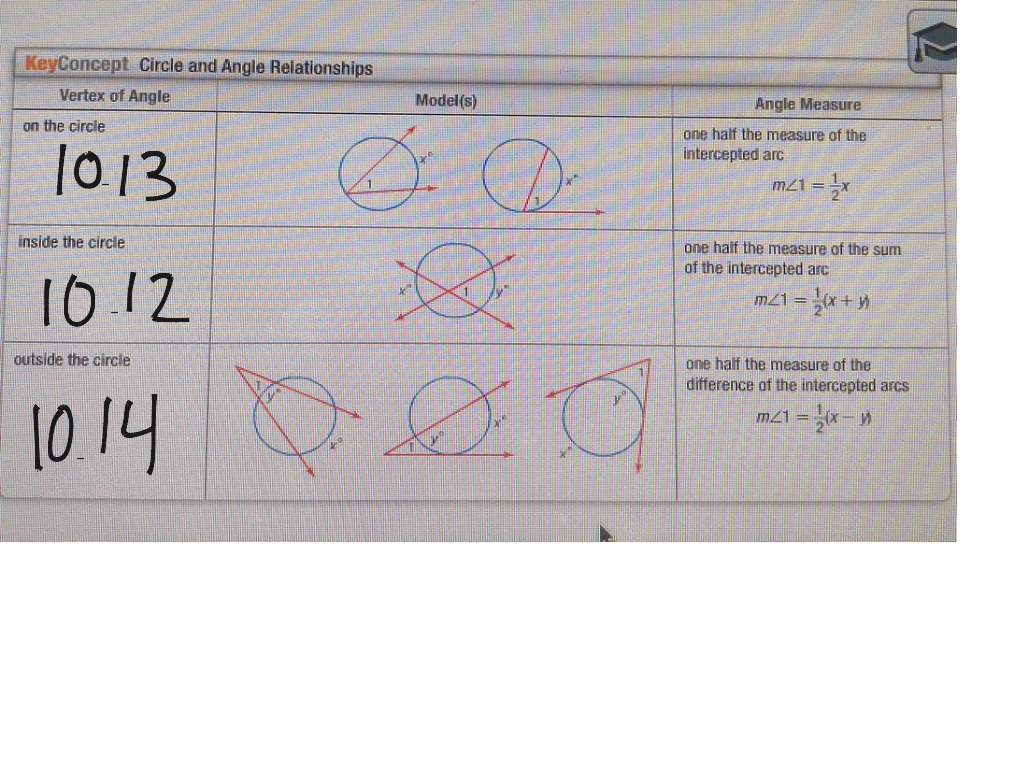
Image: www.angleworksheets.com
Angle Measures: The Key to Understanding
Imagine a circle with intersecting secants, tangents, or even a combination of both. At each point where these lines cross, angles emerge. These angles are the key to unlocking the relationships between lines and the circle. By applying the right theorems and formulas, we can calculate their precise measurements.
Essential Theorems: Unveiling the Relationships
The Tangent-Secant Angle Theorem
This theorem states that if a tangent and a secant intersect at a point outside a circle, the measure of the angle formed is half the difference between the two intercepted arcs. This theorem provides a powerful tool for calculating unknown angles.
For example, imagine you have a circle with a tangent and a secant intersecting at a point outside the circle. The tangent intercepts an arc of 60 degrees, while the secant intercepts an arc of 120 degrees. Using the Tangent-Secant Angle Theorem, we can determine the angle formed by the intersection is half the difference between the two intercepted arcs: (120 – 60) / 2 = 30 degrees.
The Intersecting Secants Theorem
If two secants intersect inside a circle, the measure of the angle formed is half the sum of the two intercepted arcs. This theorem provides another way to calculate angle measures within a circle.
Imagine two secants intersecting inside a circle, intercepting arcs of 80 degrees and 100 degrees. The angle formed by the intersecting secants is half the sum of these two intercepted arcs: (80 + 100) / 2 = 90 degrees. This theorem helps us understand that even within a circle, angles can have surprising relationships.
Putting it all Together: Practice Time!
Now let’s dive into some practice problems to solidify our understanding of secants, tangents, and angle measures.
Practice Problem 1:
A tangent and a secant intersect at a point outside a circle. The tangent intercepts an arc of 40 degrees, and the secant intercepts an arc of 100 degrees. What is the measure of the angle formed by the intersection?
Solution:
Using the Tangent-Secant Angle Theorem: (100 – 40) / 2 = 30 degrees. Therefore, the angle formed by the intersection is 30 degrees.
Practice Problem 2:
Two secants intersect inside a circle, intercepting arcs of 60 degrees and 120 degrees. What is the measure of the angle formed by the intersection of the secants?
Solution:
Using the Intersecting Secants Theorem: (60 + 120) / 2 = 90 degrees. The angle formed by the intersection of the secants is 90 degrees, indicating a right angle.
Beyond the Textbook: Applications in the Real World
The principles of secants, tangents, and angle measures transcend theoretical exercises. They have practical applications in various fields, including:
- Architecture: Architects use these concepts when designing circular structures like domes, arches, and curved staircases. They ensure stability and optimize space within these structures by understanding how lines and angles interact around a circle.
- Engineering: Engineers rely on these concepts to design circular gears, pulleys, and other mechanical components, optimizing motion transfer and efficiency.
- Astronomy: Astronomers use similar principles to analyze the paths of celestial objects like satellites and planets, studying their orbits and positions relative to Earth.
- Navigation: Sailors and pilots use these principles to navigate using compass bearings, understanding how lines of longitude and latitude intersect around the globe.
These are just a few examples showing how these seemingly abstract concepts directly impact our lives. Further exploration in this field unveils their relevance across diverse industries, proving that geometry is far from just an academic pursuit.
10 6 Practice Secants Tangents And Angle Measures
https://youtube.com/watch?v=Zk6cEDdlKPk
Expanding Your Knowledge: Resources and Further Exploration
Now that you have a foundation in secants, tangents, and angle measures, there are numerous resources available for expanding your knowledge. Explore online interactive tutorials, engaging geometry textbooks, or even consider taking specialized courses in geometry or related disciplines. Engage with like-minded individuals through online forums and discussion groups to share ideas and challenges.
As you delve deeper into these concepts, remember that they are not isolated elements but connect to a broader framework of geometry. This framework helps us understand the world around us, empowering us to make rational decisions and solve problems with greater clarity. So, continue your journey, and let the world of secants, tangents, and angle measures unveil its incredible potential.






