Do you remember the nervous energy, the flurry of calculations, and the all-too-short time limit of the 2019 AP Calculus AB exam? If those memories send shivers down your spine, you’re not alone. Many students experience a mix of relief and anxiety after completing the exam, wondering about their performance and the elusive answers. This comprehensive guide aims to unravel the mysteries of the 2019 AP Calculus AB MCQ answers, offering insights and explanations to help you understand the reasoning behind each solution.

Image: allsatpapers.com
The AP Calculus AB exam is a critical steppingstone for aspiring mathematicians, engineers, and scientists. Its multiple-choice questions (MCQs) account for a significant portion of the total exam score, thus understanding the underlying principles and problem-solving strategies behind these questions is crucial. This guide delves into the intricacies of the 2019 AP Calculus AB MCQ answers, providing a detailed analysis of each question and its corresponding solution. With a focus on clarity, accuracy, and real-world applications, this resource equips you with the knowledge and tools to confidently navigate the intricacies of calculus.
Understanding the 2019 AP Calculus AB MCQ Structure
The 2019 AP Calculus AB exam consisted of two sections: a multiple-choice section and a free-response section. The multiple-choice section contained 45 questions, each worth 1 point, and was divided into two parts:
- Part A: This part comprised 30 multiple-choice questions with no calculator allowed, testing fundamental calculus concepts like limits, derivatives, integrals, and applications of these concepts.
- Part B: This part included 15 multiple-choice questions that permitted the use of a graphing calculator, emphasizing a deeper understanding of calculus concepts and their practical applications.
The 2019 AP Calculus AB MCQ answers were initially kept confidential, only released to teachers and students after the scoring process concluded. However, over time, some resources have emerged online that offer insights into the solutions of the 2019 exam’s MCQ section. This guide will provide a valuable resource for analyzing these solutions and understanding their underlying principles.
Dissecting the 2019 AP Calculus AB MCQ Answers: A Deep Dive
To effectively analyze the 2019 AP Calculus AB MCQ answers, a systematic approach is essential. We will explore each MCQ question based on its topic, the underlying concept, and the correct solution. This detailed breakdown will reveal the reasoning behind each answer, providing a comprehensive understanding of the questions and their solutions.
Section I: Part A: Non-Calculator Questions
This section covered a wide range of fundamental calculus concepts, testing your understanding of the building blocks of differential and integral calculus. Let’s delve into some of the key areas tested in this section and the strategies used to solve these problems:
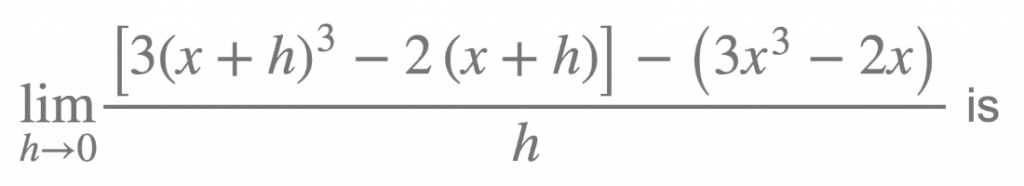
Image: collegeprep.uworld.com
1. Limits and Continuity
Understanding limits and continuity is crucial for the foundation of calculus. The 2019 exam featured several questions evaluating your ability to determine limits, analyze continuity, and apply limit laws. To solve these problems, it’s essential to be familiar with the different types of limits (one-sided, two-sided), the definition of continuity, and the concept of removable discontinuity. Consider the following example:
2. Derivatives and Their Applications
Derivatives are used to measure the instantaneous rate of change, which is crucial for analyzing motion, optimization, and related rates problems. This section tested your knowledge of derivative rules (e.g., power rule, product rule, chain rule) and how to apply them in various contexts. A representative example would be:
3. Integrals and Their Applications
Integration enables the calculation of areas, volumes, and other accumulation quantities. The 2019 exam contained questions on definite and indefinite integrals, the fundamental theorem of calculus, and applications of integration to real-world situations. Examining the following problem can help illustrate these concepts:
Section I: Part B: Calculator-Active Questions
This section leveraged the power of graphing calculators to explore more complex calculus problems. Calculator-assisted questions focused on visual interpretations of graphs, numerical integration techniques, and real-world applications. Here are some examples of common calculator-active questions:
1. Graph Analysis and Interpretation
These questions required you to analyze the graph of a function and its derivatives, interpreting features like local extrema, inflection points, and concavity. A typical example could be:
2. Numerical Integration and Approximation
Graphing calculators are invaluable for approximating definite integrals using techniques like the trapezoidal rule or Simpson’s rule. Understanding these methods and applying them effectively using a calculator is crucial. Consider the following:
3. Real-World Applications and Modeling
The final section used calculus to model real-world phenomena like motion, population growth, and economics. By applying concepts like differential equations and optimization, you could analyze complex scenarios and arrive at meaningful conclusions. An illustrative example would be:
Strategies for Success: Tackling the 2019 AP Calculus AB MCQ Answers
Understanding the 2019 AP Calculus AB MCQ answers is invaluable, but it’s equally important to develop effective strategies for tackling future exam questions. Here are some key strategies to enhance your performance:
- Master Fundamental Concepts: A solid grasp of limits, derivatives, integrals, and their applications is crucial. Practice solving various problems to solidify your understanding and develop intuition for different concepts.
- Practice with Past Exams: Familiarize yourself with the exam format, question types, and difficulty levels. Past exam papers provide valuable practice, allowing you to identify your strengths and weaknesses.
- Learn Effective Time Management: The time limit for the MCQ section is strict, so manage your time wisely. Start with questions you’re most confident about and avoid spending too long on any single question.
- Develop Calculator Proficiency: For questions requiring calculator usage, practice using your graphing calculator efficiently. Familiarize yourself with its capabilities, including graphing functions, calculating derivatives, and finding numerical integrals.
- Apply Math to Real-World Scenarios: Practicing problems that connect calculus concepts to real-world applications can help you develop a deeper understanding and improve your problem-solving skills.
2019 Ap Calc Ab Mcq Answers
Conclusion: Navigating the World of Calculus with Confidence
Understanding the 2019 AP Calculus AB MCQ answers is a stepping stone on your journey through the fascinating world of calculus. This guide has provided a comprehensive analysis of the concepts, solutions, and strategies related to these questions. Armed with this knowledge, you can approach future exams with confidence, knowing how to approach these questions and applying your understanding to solve challenging problems. Remember that calculus is a dynamic and ever-evolving field, and continuous learning is key to unlocking its full potential. Embrace the challenges and the rewards of this captivating subject, and enjoy the journey of exploring its vast applications in various scientific disciplines and real-world situations.






