Remember those frustrating geometry problems in school? The ones that involved calculating volume, and especially those that required you to grapple with the shapes of prisms and cylinders? I sure do! It seemed like a confusing maze of formulas and numbers, and I often found myself wondering where to even begin. But, as they say, practice makes perfect, and that’s where worksheets come in. These little guides can be lifesavers for learning and understanding how to find the volume of various geometric shapes – especially for prisms and cylinders.

Image: materiallibmeyer.z19.web.core.windows.net
Today, we’re going to explore the world of volume calculations for prisms and cylinders. We’ll demystify the workings of those baffling worksheets, uncover the secrets of volume formulas, and reveal the tricks to mastering these geometric concepts. Get ready to conquer those challenging problems and take your understanding of volume to the next level!
Understanding Volume: The Essence of Three-Dimensional Space
Volume, in simple terms, represents the amount of space a three-dimensional object occupies. Imagine a box filled with marbles. The volume of that box is the total amount of space those marbles take up. It’s similar to how we measure the capacity of containers – like the amount of liquid a bottle can hold.
For prisms and cylinders, the volume calculation helps us understand how much material is needed to fill the entire space within their shape. Whether it’s the amount of sand in a cylindrical sandbox or the volume of air in a rectangular room, understanding volume provides essential information for various real-world applications.
Unveiling the Formulas: Decoding the Volume of Prisms and Cylinders
Before we dive into the worksheets, let’s unpack the essential formulas for calculating the volume of prisms and cylinders.
Volume of a Prism
A prism is a three-dimensional shape with two identical bases that are parallel to each other, connected by rectangular faces. Think of a rectangular box or a triangular prism. To find the volume of any prism, you use a simple formula:
Volume (Prism) = Base Area × Height
Let’s break it down. The base area refers to the area of one of the identical bases. It could be a rectangle, a triangle, a square, or a hexagon, depending on the prism’s shape. The height, on the other hand, is the perpendicular distance between those two bases.
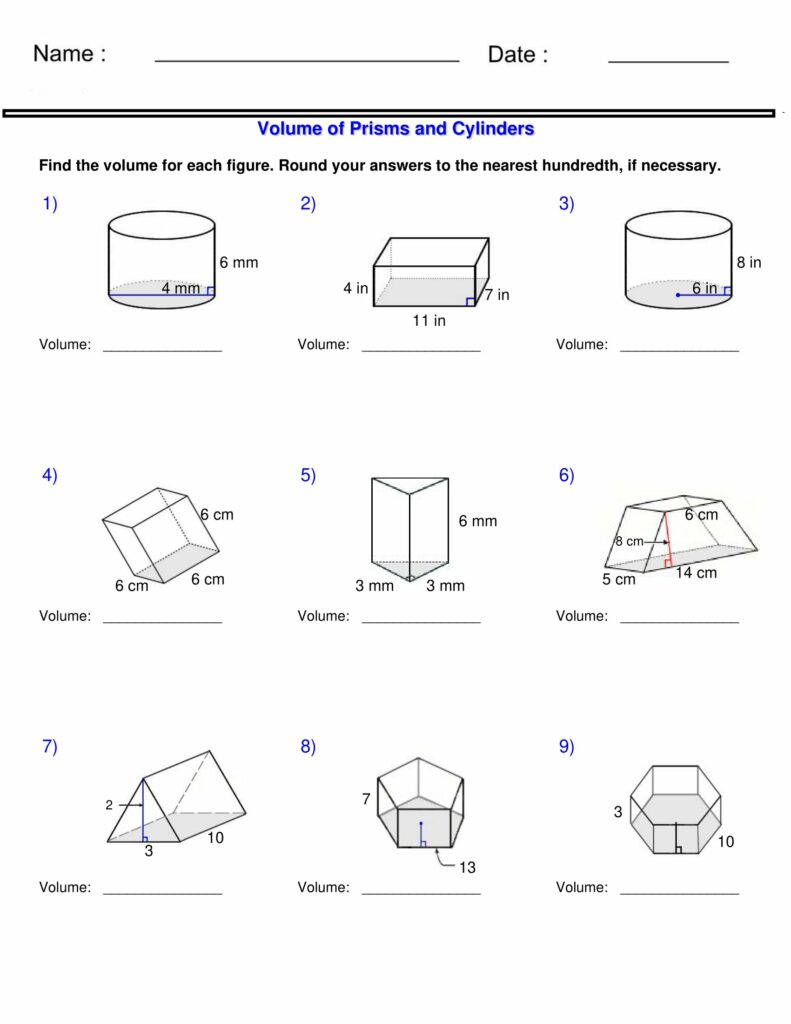
Image: www.madebyteachers.com
Volume of a Cylinder
A cylinder, on the other hand, is a three-dimensional shape with two parallel and congruent circular bases connected by a curved surface. Think of a soup can or a rolling pin. Like prisms, the volume of a cylinder is calculated using a straightforward formula:
Volume (Cylinder) = Base Area × Height
Here, the base area is the area of each circular base, calculated by the formula:
Base Area (Circle) = π × r², where π is approximately 3.14 and r is the radius of the circle. The height is the perpendicular distance between the two bases.
Decoding Volume Worksheets: Unlocking the Secrets of Solutions
Now, let’s move on to the actual worksheets. They are often designed to guide you through a series of problems, helping you practice calculating the volume of prisms and cylinders. Here’s a breakdown of how to tackle them effectively.
Typically, a volume worksheet will present you with a diagram of a prism or cylinder. The dimensions of the shape – length, width, height, radius, or side lengths – will be provided. Your task is to calculate the volume using the formulas we’ve discussed. Here’s a step-by-step approach to mastering those worksheets.
1. Identify the Shape
Begin by determining whether the shape is a prism or a cylinder. Once you’ve identified the shape, you’ll know which formula to use.
2. Identify the Dimensions
Carefully examine the diagram and note the provided dimensions. These might include length, width, height, radius, or side lengths. Make sure to write them down so you don’t miss any crucial information.
3. Apply the Correct Formula
Now, it’s time to apply the appropriate volume formula. For a prism, use the formula: Volume (Prism) = Base Area × Height. If it’s a cylinder, use: Volume (Cylinder) = Base Area × Height.
4. Calculate the Base Area
For prisms, the base area depends on the shape of the base. For a rectangular base, you’d calculate Area = length × width. For a triangular base, you’d use the formula Area = (1/2) x base x height. For cylinders, calculate the base area using Base Area (Circle) = π × r².
5. Complete the Volume Calculation
Now that you have the base area and the height (for prisms and cylinders), simply multiply them together to obtain the volume. Remember to use the correct units of measurement.
6. Double-Check Your Work
Before marking your answer, take a moment to review your calculations. Make sure you haven’t missed any steps or made any errors in your arithmetic.
Mastering the Art of Volume: Pro Tips for Success
Here are some professional tips to help you really excel in calculating volume:
Practice Makes Perfect
The key to mastering any mathematical concept is consistent practice. The more you work through volume worksheets and problems, the more comfortable you’ll become with the formulas and the easier it will be to apply them. Don’t hesitate to go back and try different variations of the problems to reinforce your understanding.
Visualize the Shape
Sometimes, it helps to visualize the 3D shape in your mind’s eye. Imagine holding the prism or cylinder in your hands. This can help you better understand the relationship between the dimensions and the volume.
Break It Down
If a problem seems overwhelming, don’t be afraid to break it down into smaller, more manageable steps. For example, calculate the base area separately before plugging it into the final volume formula. This approach can significantly reduce the chance of errors.
Frequently Asked Questions: Solving Common Doubts
Q: What are the units for volume?
A: The units for volume are cubic units, such as cubic centimeters (cm³), cubic meters (m³), or cubic feet (ft³).
Q: How do I handle different units in my calculations?
A: If you have different units of measurement in your problem (e.g., cm and mm), you need to convert them to a single consistent unit before you make your calculations.
Q: What are some common applications of volume calculations in the real world?
A: Volume calculations are used extensively in various fields:
– **Construction:** Calculating the volume of a room or building to determine the amount of materials needed.
– **Engineering:** Designing and building structures, machines, and vehicles.
– **Medical:** Measuring fluid volumes for patients.
– **Physics:** Understanding concepts like density and buoyancy.
– **Chemistry:** Calculating the volume of liquids and gases in reactions and experiments.
Volume Of Prisms And Cylinders Worksheet Answers
Conclusion: Unlocking the World of Volume
We’ve journeyed into the realm of volume calculations for prisms and cylinders, demystifying the formulas and conquering the challenges of worksheets. With practice, patience, and a good understanding of the concepts, you’ll be a volume master in no time. Remember, the key is to practice regularly, visualize the shapes, and break down complex problems into smaller, manageable steps. Are you ready to tackle those volume problems? Let’s dive in and unlock your geometric potential!






